Diamonds - Part 2 - A cut above - Building Linear Models
In a previous post in this series, we did an exploratory data analysis of the diamonds dataset and found that carat, x, y, z were strongly correlated with price. To some extent, clarity also appeared to provide some predictive ability.
In this post, we will build linear models and see how well they predict the price of diamonds.
Before we do any transformations, feature engineering or feature selections for our model, let’s see what kind of results we get from a base linear model, that uses all the features to predict price:
Call:
lm(formula = price ~ ., data = diamonds)
Residuals:
Min 1Q Median 3Q Max
-21376 -592 -183 376 10694
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5753.76 396.63 14.51 < 0.0000000000000002 ***
carat 11256.98 48.63 231.49 < 0.0000000000000002 ***
cut.L 584.46 22.48 26.00 < 0.0000000000000002 ***
cut.Q -301.91 17.99 -16.78 < 0.0000000000000002 ***
cut.C 148.03 15.48 9.56 < 0.0000000000000002 ***
cut^4 -20.79 12.38 -1.68 0.0929 .
color.L -1952.16 17.34 -112.57 < 0.0000000000000002 ***
color.Q -672.05 15.78 -42.60 < 0.0000000000000002 ***
color.C -165.28 14.72 -11.22 < 0.0000000000000002 ***
color^4 38.20 13.53 2.82 0.0047 **
color^5 -95.79 12.78 -7.50 0.000000000000066 ***
color^6 -48.47 11.61 -4.17 0.000030090737193 ***
clarity.L 4097.43 30.26 135.41 < 0.0000000000000002 ***
clarity.Q -1925.00 28.23 -68.20 < 0.0000000000000002 ***
clarity.C 982.20 24.15 40.67 < 0.0000000000000002 ***
clarity^4 -364.92 19.29 -18.92 < 0.0000000000000002 ***
clarity^5 233.56 15.75 14.83 < 0.0000000000000002 ***
clarity^6 6.88 13.72 0.50 0.6157
clarity^7 90.64 12.10 7.49 0.000000000000071 ***
depth -63.81 4.53 -14.07 < 0.0000000000000002 ***
table -26.47 2.91 -9.09 < 0.0000000000000002 ***
x -1008.26 32.90 -30.65 < 0.0000000000000002 ***
y 9.61 19.33 0.50 0.6192
z -50.12 33.49 -1.50 0.1345
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1130 on 53916 degrees of freedom
Multiple R-squared: 0.92, Adjusted R-squared: 0.92
F-statistic: 2.69e+04 on 23 and 53916 DF, p-value: <0.0000000000000002# A tibble: 3 x 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 rmse standard 1130.
2 rsq standard 0.920
3 mae standard 740. The model summary shows it is an overfitted model. Among other things, we know that depth and table have no impact on price, yet these are shown to be highly significant. Root Mean Squared Error (rmse) and other metrics are also shown above.
Let’s make a plot of actual v/s predicted prices to visualize how well this base model performs.
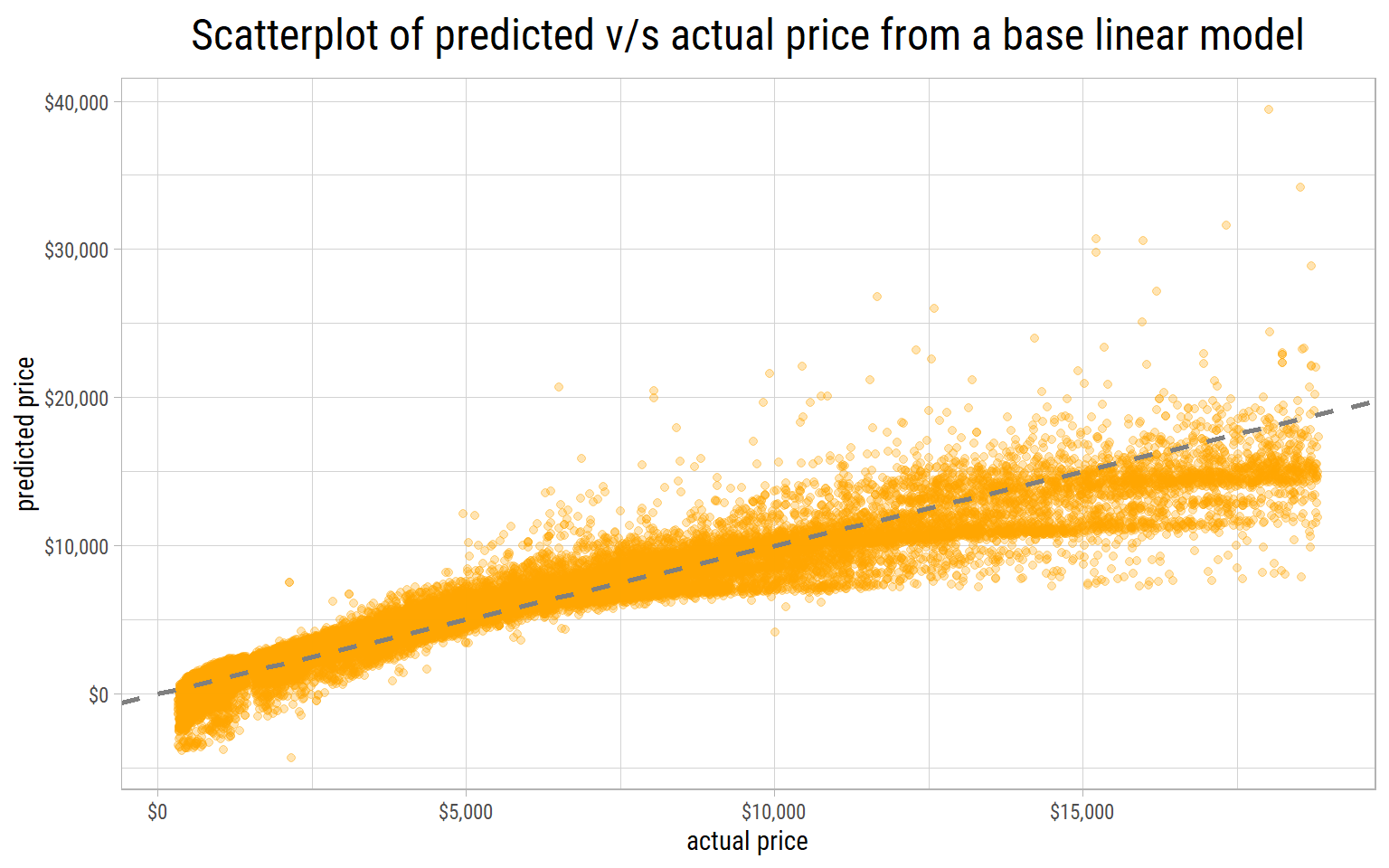
If the predictions are good, the points should lie close to a straight line drawn at 45 degrees. We can see this base model does a poor job of predicting prices. Worst of all, the model predicts negative prices on the lower end.
It shows that price has to be log transformed to avoid these absurdities.
Feature Engineering
We know the price of a diamond is strongly correlated with its size. All things equal, the larger the diamond, the greater its price.
As a first approximation, we can assume a diamond is a cuboid with dimensions x, y and z. Then, we can compute its volume as x * y * z.
As these 3 dimensions are highly correlated, we can compute a geometrical average dimension by taking the cube root of volume, and retain a linear relationship with log(price).
Another way to calculate an average dimension is by using high school chemistry. Mass, volume and density are related to each other by the equation:
$ density = mass/volume $
We can find out that 1 carat = 0.2 gms. Dividing by the density of diamond (3.51 gms/cc) would give us its volume in cc, which could be converted to a geometrical average dimension by taking the cube root.
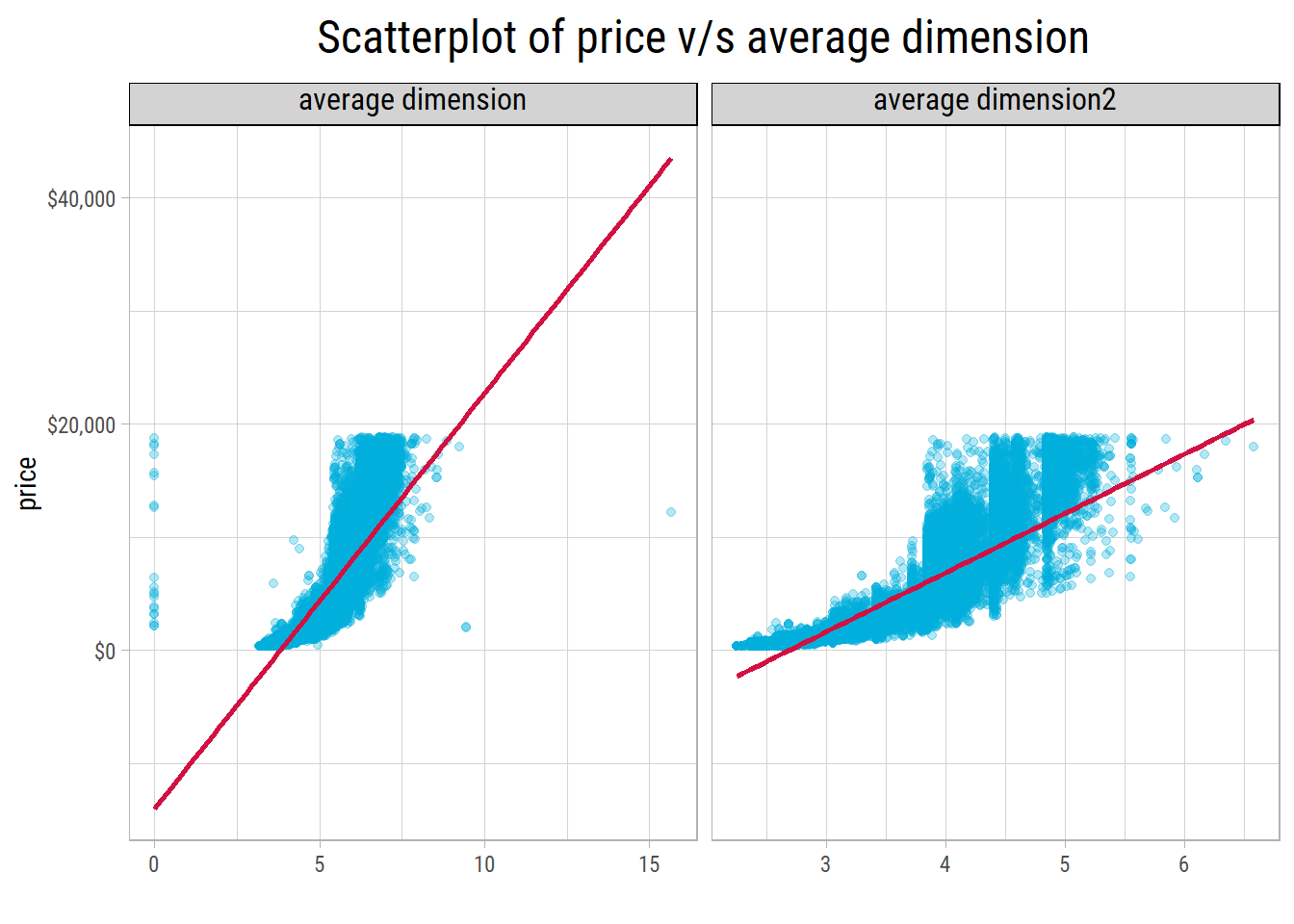
Even though both methods yield similar results, we could see that the density method results in a narrower range. But which method would be more robust?
Keep in mind there are 20 z values that are 0. In 7 of these records both x and y are 0 too, which means these values were not recorded reliably.
# A tibble: 20 x 10
carat cut color clarity depth table price x y z
<dbl> <ord> <ord> <ord> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 1 Premium G SI2 59.1 59 3142 6.55 6.48 0
2 1.01 Premium H I1 58.1 59 3167 6.66 6.6 0
3 1.1 Premium G SI2 63 59 3696 6.5 6.47 0
4 1.01 Premium F SI2 59.2 58 3837 6.5 6.47 0
5 1.5 Good G I1 64 61 4731 7.15 7.04 0
6 1.07 Ideal F SI2 61.6 56 4954 0 6.62 0
7 1 Very Good H VS2 63.3 53 5139 0 0 0
8 1.15 Ideal G VS2 59.2 56 5564 6.88 6.83 0
9 1.14 Fair G VS1 57.5 67 6381 0 0 0
10 2.18 Premium H SI2 59.4 61 12631 8.49 8.45 0
11 1.56 Ideal G VS2 62.2 54 12800 0 0 0
12 2.25 Premium I SI1 61.3 58 15397 8.52 8.42 0
13 1.2 Premium D VVS1 62.1 59 15686 0 0 0
14 2.2 Premium H SI1 61.2 59 17265 8.42 8.37 0
15 2.25 Premium H SI2 62.8 59 18034 0 0 0
16 2.02 Premium H VS2 62.7 53 18207 8.02 7.95 0
17 2.8 Good G SI2 63.8 58 18788 8.9 8.85 0
18 0.71 Good F SI2 64.1 60 2130 0 0 0
19 0.71 Good F SI2 64.1 60 2130 0 0 0
20 1.12 Premium G I1 60.4 59 2383 6.71 6.67 0In all of these records, the carat values were recorded reliably and are probably more accurate than the dimensions.
Hence, we might prefer the density method of generating this feature.
Furthermore, since density is a constant, dividing by a constant to calculate volume isn’t really necessary. Instead, a cube root transformation could be applied to carat itself for the purposes of predictive modelling that would result in a linear relationship between \(log(price)\) and \(carat^{1/3}\).
It is the reason why we’re fitting a linear model because the model is linear in its parameters.
Training Linear Models
Here are the steps for building linear models and computing metrics:
- Partition the dataset into training and testing sets in the proportion 75% and 25% respectively.
- Since
clarityis one of the main predictors, stratify the partitioning byclarity, so both training and testing sets have the same distributions of this feature. - Fit a linear model with the training set.
- Make predictions on the testing set and determine model metrics.
- Wrap all the steps above inside a function in which the model formula and a seed could be passed. Since the seed determines the random partitioning, it helps to minimize vagaries in partitioning the training and testing sets before fitting models.
- Run multiple iterations of a model with different seeds, and compute its average metrics, that would reflect the results on unseen data.
Here’s a sample split of training and testing set, stratified by clarity. As we can see, the training and testing sets have similar distributions.
dfTrain$clarity
n missing distinct
40457 0 8
lowest : I1 SI2 SI1 VS2 VS1 , highest: VS2 VS1 VVS2 VVS1 IF
Value I1 SI2 SI1 VS2 VS1 VVS2 VVS1 IF
Frequency 552 6895 9826 9222 6125 3780 2722 1335
Proportion 0.014 0.170 0.243 0.228 0.151 0.093 0.067 0.033dfTest$clarity
n missing distinct
13483 0 8
lowest : I1 SI2 SI1 VS2 VS1 , highest: VS2 VS1 VVS2 VVS1 IF
Value I1 SI2 SI1 VS2 VS1 VVS2 VVS1 IF
Frequency 189 2299 3239 3036 2046 1286 933 455
Proportion 0.014 0.171 0.240 0.225 0.152 0.095 0.069 0.034After running 5 iterations of each model with a different seed, here are the average metrics:
# A tibble: 5 x 4
model rmse rsq mae
<chr> <dbl> <dbl> <dbl>
1 log(price) ~ . 11055. 0.670 570.
2 log(price) ~ I(carat^(1/3)) 2893. 0.687 1039.
3 log(price) ~ I(carat^(1/3)) + clarity 2312. 0.807 881.
4 log(price) ~ I(carat^(1/3)) + clarity + color 1870. 0.870 631.
5 log(price) ~ I(carat^(1/3)) + clarity + color + cut 1848. 0.875 625.The first model with all predictors is an overfitted one.
The model with carat, clarity and color provides the best combination of root mean squared error and r-squared, that explains the most variance.
This is our final model.
Including cut in the model has diminishing benefits, and tends to overfit the data.
Here’s the summary of our final model:
Call:
lm(formula = model_formula, data = dfTrain)
Residuals:
Min 1Q Median 3Q Max
-1.6022 -0.1034 0.0145 0.1066 1.7941
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.147009 0.004993 429.99 < 0.0000000000000002 ***
I(carat^(1/3)) 6.246412 0.005365 1164.27 < 0.0000000000000002 ***
clarity.L 0.922295 0.005036 183.15 < 0.0000000000000002 ***
clarity.Q -0.295539 0.004734 -62.43 < 0.0000000000000002 ***
clarity.C 0.166979 0.004068 41.05 < 0.0000000000000002 ***
clarity^4 -0.068591 0.003260 -21.04 < 0.0000000000000002 ***
clarity^5 0.032833 0.002669 12.30 < 0.0000000000000002 ***
clarity^6 -0.001904 0.002325 -0.82 0.41288
clarity^7 0.025508 0.002049 12.45 < 0.0000000000000002 ***
color.L -0.488882 0.002927 -167.05 < 0.0000000000000002 ***
color.Q -0.117319 0.002680 -43.78 < 0.0000000000000002 ***
color.C -0.012230 0.002497 -4.90 0.00000098 ***
color^4 0.019007 0.002288 8.31 < 0.0000000000000002 ***
color^5 -0.008110 0.002159 -3.76 0.00017 ***
color^6 -0.000396 0.001967 -0.20 0.84055
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.166 on 40442 degrees of freedom
Multiple R-squared: 0.973, Adjusted R-squared: 0.973
F-statistic: 1.05e+05 on 14 and 40442 DF, p-value: <0.0000000000000002
Here’s a scatterplot of actual v/s predicted log(price) from our final model on the testing set:
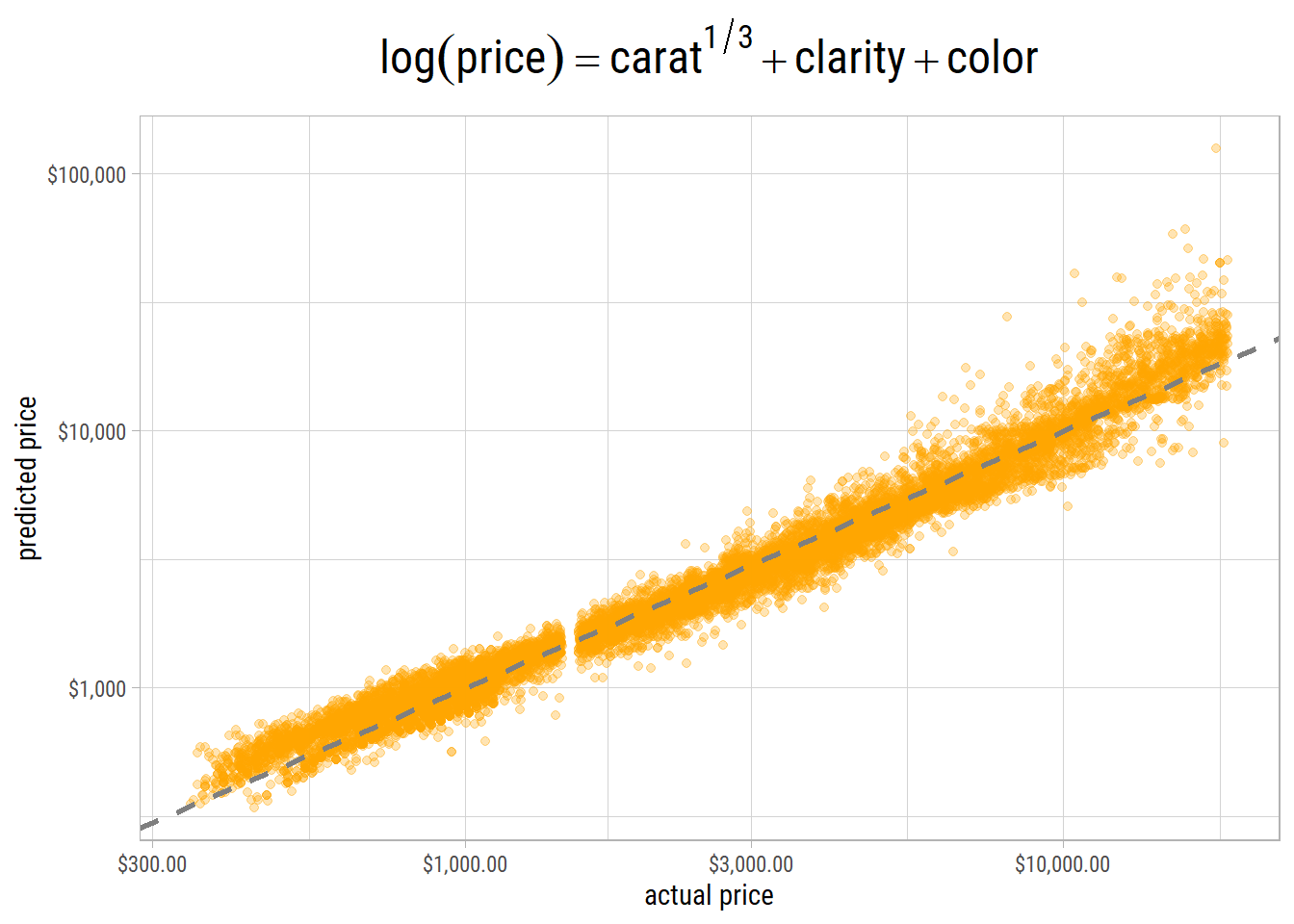
The points lie close to the 45 degress line. However, on the high end, there are many outliers where actual and predicted values have very high variance. Nevertheless, this is as good as it gets.